什么是描述性统计方法?
什么是描述性统计方法?

描述性统计方法是用来分析连续数据的分布特性。
当项目团队从过程中抽样并获得样本数据后,需要对数据分布情况有基本了解。如:
❑ 分布的位置或者中心趋势
❑ 数据的散布程度
❑ 分布的形状
样本统计量
常用的统计量分为两类:
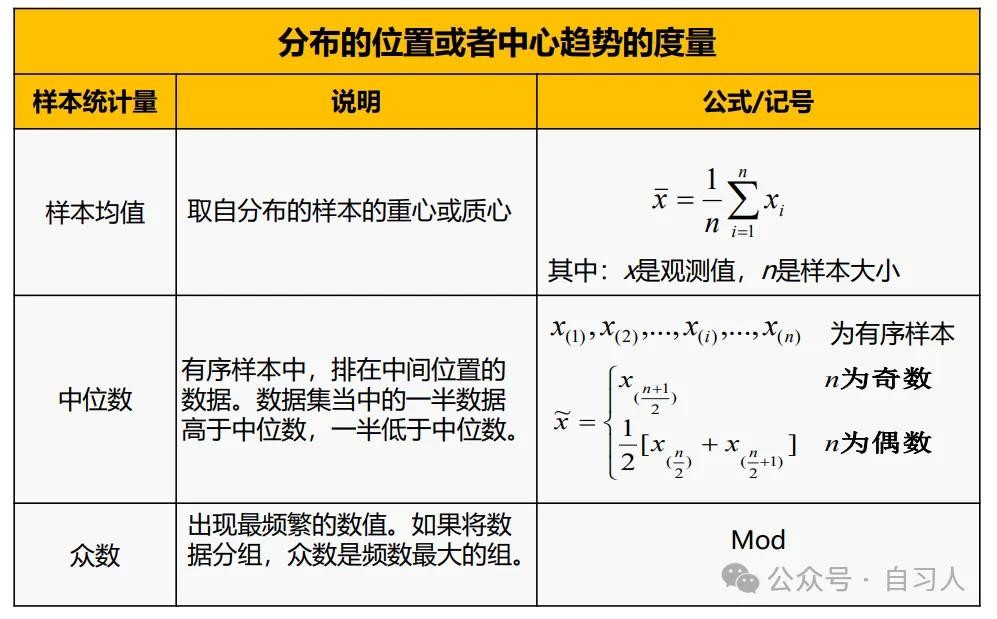
❑ 表示分布位置的量
— 如平均值、中位数、众数等
❑ 表示分布的分散程度的量
— 如样本方差、样本标准差、极差、以及变异系数等
用样本统计量描述分布的中心趋势和分散程度
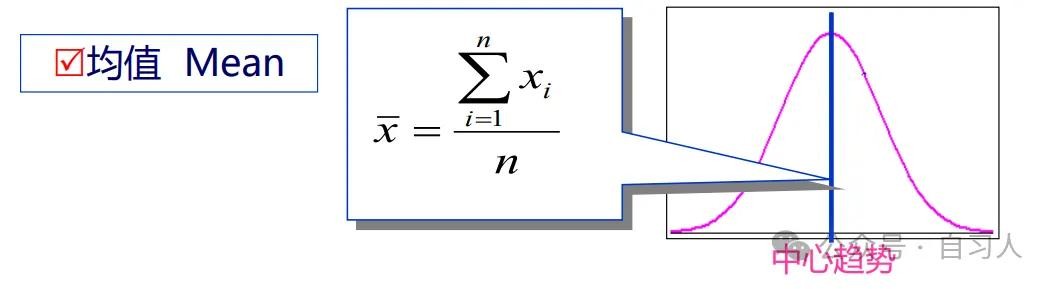

样本均值
样本均值刻画了样本数据的平均水平,是估计总体均值μ 的一个常用统计量
设一组样本为 y1 , y2 , …, yn ,则它的样本均值为
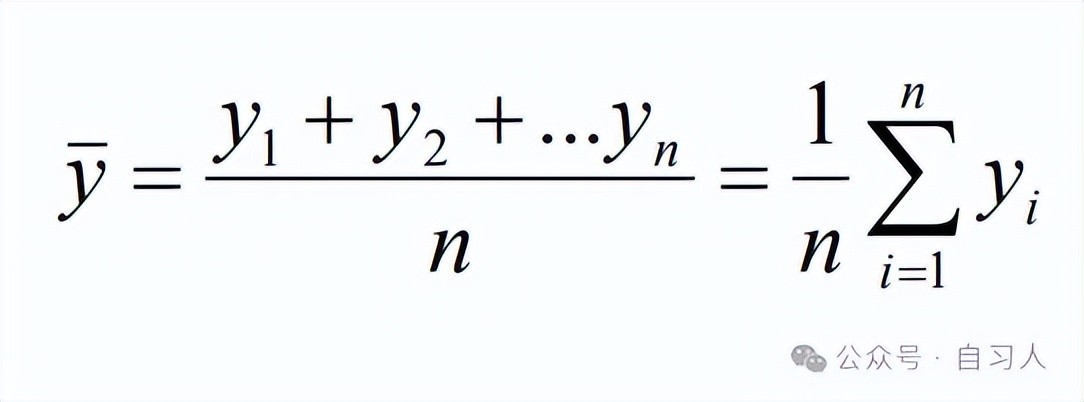
样本中位数
用来估计分布中心位置的统计量。将样本数据按大小顺序重新排列,位于中间位置的数值,就称为中位数,有时也称为中值
设一组样本为 x1 , x2 ,…, xn,则它的样本中位数为:
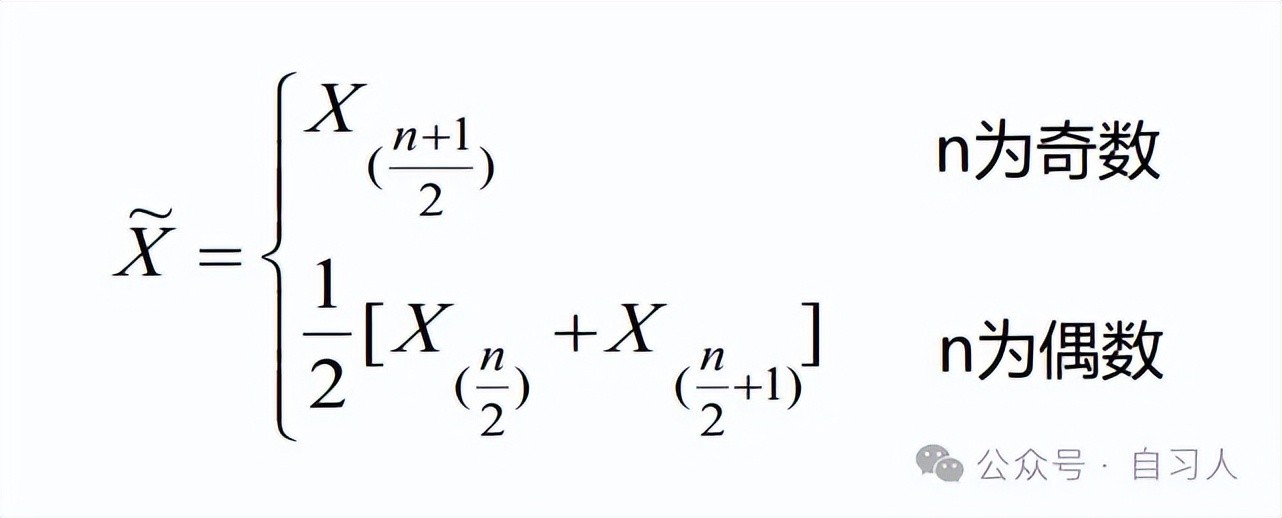
样本极差
极差是用来度量样本数据分散程度的常用统计量,它是样本数据中最大值与最小值的差值,一般用字母R表示。
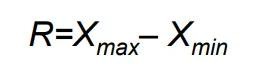
样本方差
样本方差刻画了样本数据的波动大小,是估计总体方差σ²的一个常用统计量,一般用符号S²表 示 。 称它的平方根为样本标准差。
设一组样本为 y1 , y2 , …, yn ,则它的样本方差为:
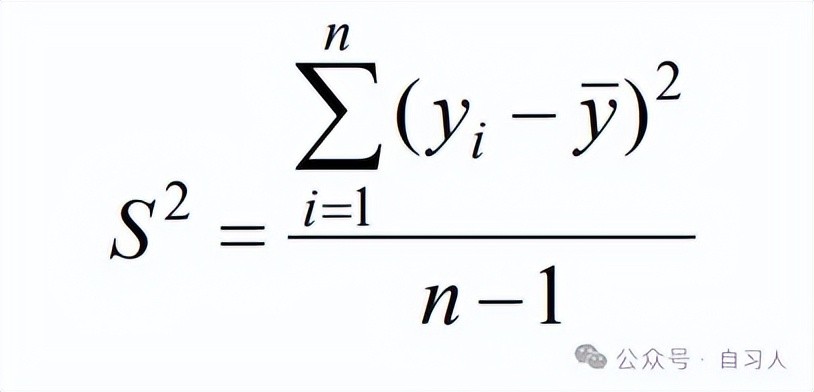
计算公式
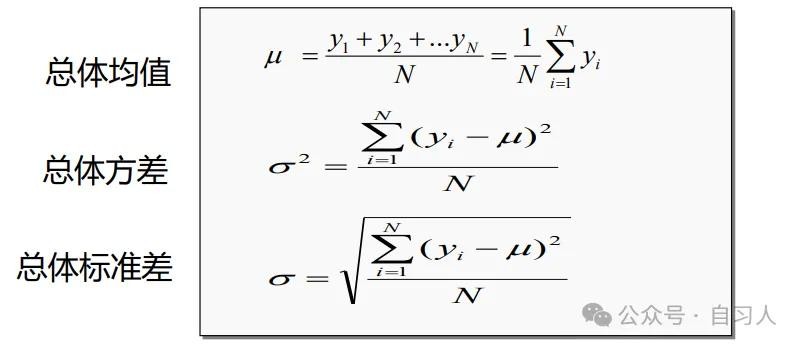
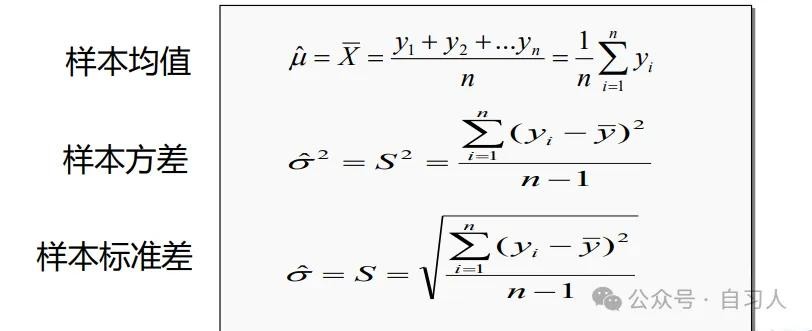
描述性统计汇总表-分布位置
描述性统计汇总表-分散程度
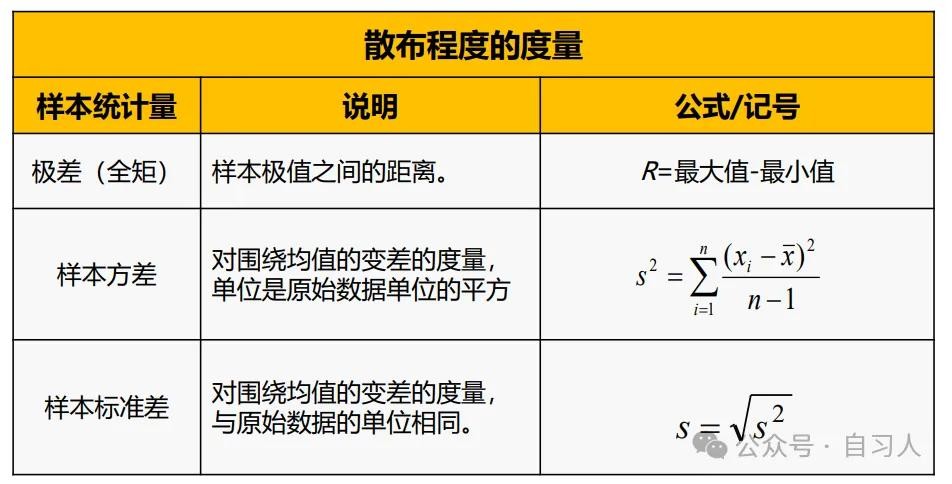
描述性统计汇总表-分布形状
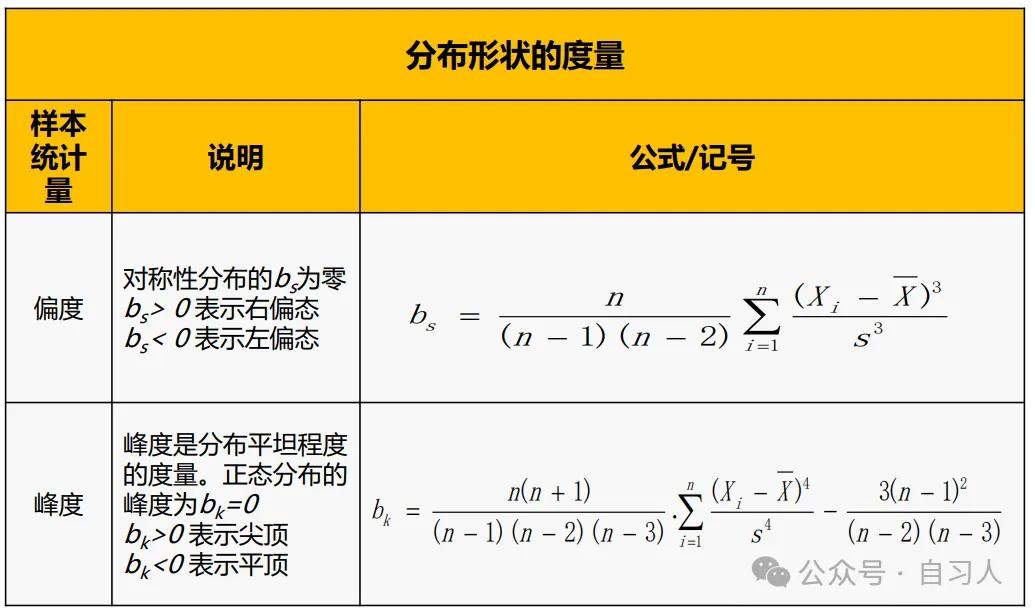
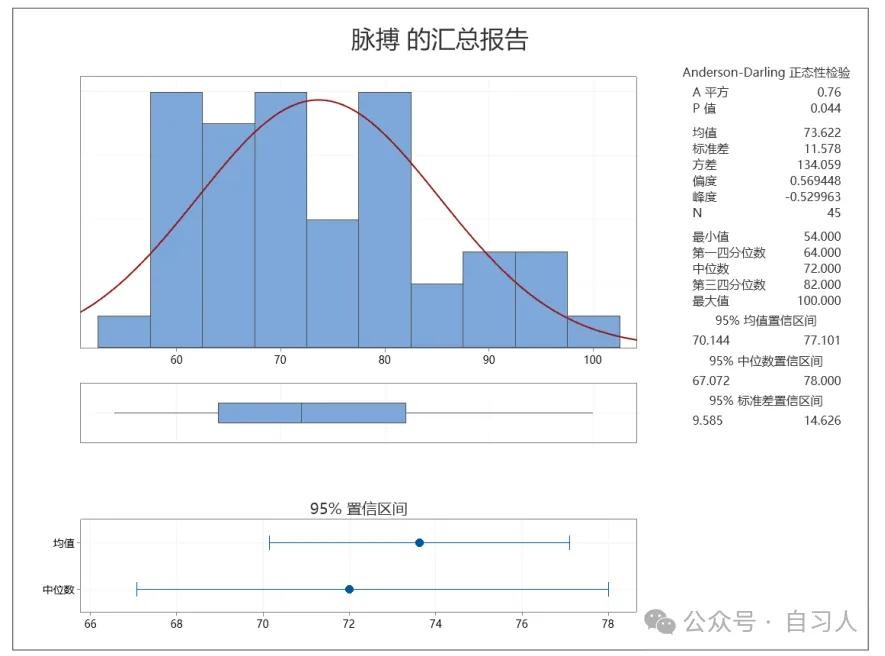
描述性统计分析——图形化汇总
❑ 描述性统计方法是帮助我们对数据分布情况作出基本了解的手段
❑ 常用的描述分布的位置或中心趋势的样本统计量有:样本均值、样本中位数和众数
❑ 常用的描述分布的分散程度的样本统计量有:样本极差、样本方差和样本标准差
❑ 常用的描述分布形状的样本统计量有:偏度和峰度
本文知识点2024年六西格玛黑带考了两道题,让我们来看看
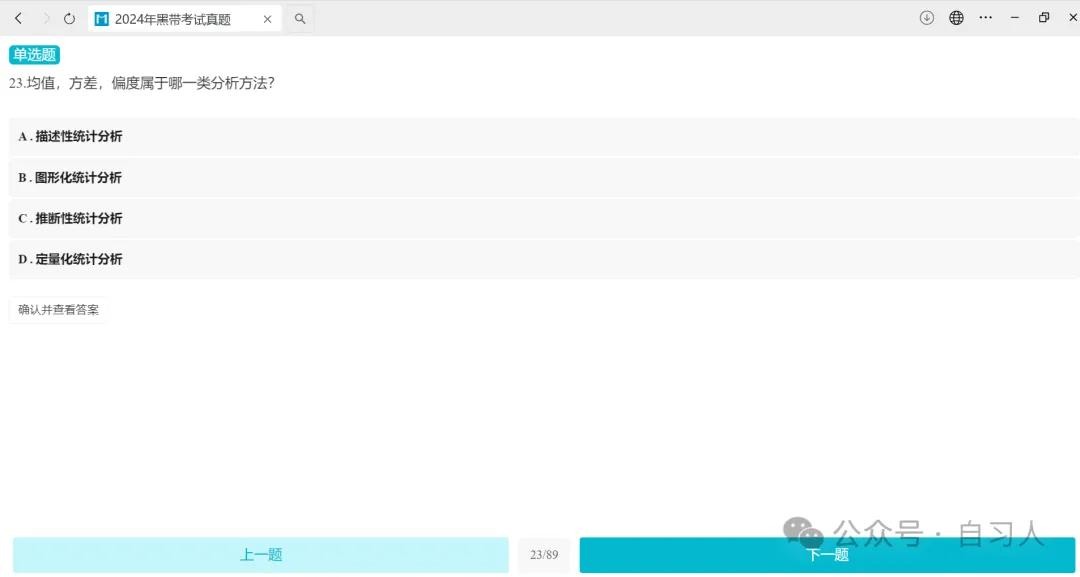
大家可以在留言板写下答案,
-

- 喝酒划拳时喊的“五魁首,六六六”,是什么意思?
-
2025-12-26 06:23:05
-

- 天蝎女不理你说明什么?一般代表这三个意思播报
-
2025-12-26 06:21:01
-

- 洗龙沟是什么?给皇帝“洗龙沟”,到底有何特殊的地方?
-
2025-12-25 08:19:08
-
- 煤改电又是咋回事?怎么改?注意什么?
-
2025-12-25 08:17:05
-

- 传说中的“象冢”真的存在吗?大象在即将死去的时候会做什么?
-
2025-12-25 08:14:59
-

- 河南的小伙伴收过这样的短信吗?带大家了解下什么是对口援疆
-
2025-12-25 08:12:54
-

- 郭靖黄蓉一生究竟经历了什么?将三个孩子的名字连起来读就明白了
-
2025-12-25 08:10:50
-

- 什么是CG?
-
2025-12-25 08:08:46
-
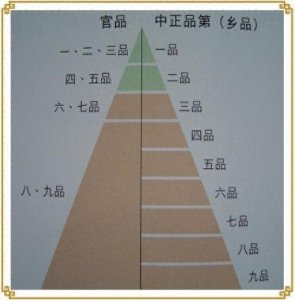
- 魏晋时期的九品中正制是如何发展的,又有什么弊端?
-
2025-12-25 08:06:42
-

- 什么叫碑帖?如何学习碑帖?有哪些碑帖推荐?我都讲给你听
-
2025-12-25 08:04:37
-

- 大家热衷谈论的“仪式感”究竟是什么?
-
2025-12-25 08:02:33
-

- 2022银行招聘考试:银行笔试怎么准备?各大银行考试有什么不同?
-
2025-12-25 08:00:28
-

- 四太梁安琪被曝400亿身价:赌王去世,她凭什么成为最大赢家?
-
2025-12-24 09:41:02
-

- 酸枝是什么木头?哪些才是真正的酸枝?
-
2025-12-24 09:38:58
-

- 陈丽华为什么出生在颐和园,她是慈禧的什么人,跟溥仪有什么关系
-
2025-12-24 09:36:54
-

- 周继红:开除田亮、培养全红婵,把郭晶晶送到裁判席,她什么来头
-
2025-12-24 09:34:49
-

- 扫黑除恶小知识 | 什么是“黑”?什么是“恶”?
-
2025-12-24 09:32:45
-
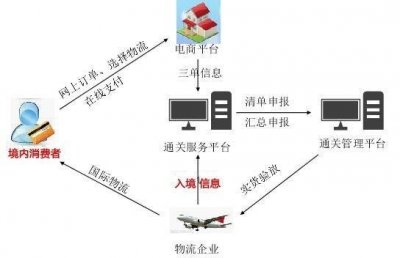
- 近几年一直在火的,“跨境电商”,他到底是什么呢
-
2025-12-24 09:30:41
-

- 有多少人了解弥勒菩萨和弥勒佛究竟有什么不同?
-
2025-12-24 09:28:36
-

- 地表最强轻步兵:侦察连敢鄙视警卫连,什么白虎黑豹通通一锅端!
-
2025-12-24 09:26:32


 马云评价任正非 用8个字评价华为创始人
马云评价任正非 用8个字评价华为创始人 100毫升水参照物
100毫升水参照物